Wenn man im Frühjahr 2010 nach der Wahrscheinlichkeit der im Juli 2010 im Moskau tatsächlich gemessenen Durchschnittstemperatur, oder einer höheren Temperatur, gefragt hätte, dann wäre von Experten mit Hinweis auf die in der Vergangenheit gemessenen Durchschnittstemperaturen eine Wahrscheinlichkeit von weniger als 1 zu 15000 genannt worden. Das heißt, man hätte gemeint, nur einmal in mehr als 15.000 Jahren, und damit so gut wie nie, könnte eine solch hohe Durchschnittstemperatur erreicht werden, wie sie dann tatsächlich gemessen wurde. Zu den politischen Folgen gehörte auch der “Arabische Frühling”. Wie ist so etwas möglich? Was den “Arabischen Frühling”, also die Unruhen im Nahen Osten und in Nordafrika angeht, so gehörte zu den Ursachen auch der Anstieg der Lebensmittelpreise, zu dem es u.a. kam, weil Russland als Folge der Hitzewelle im Sommer 2010 den Export von Getreide gestoppt hatte. Die Wirklichkeit ist auch hier ziemlich komplex. Von www.americanprogress.org gibt es dazu ein 68-seitiges Papier mit dem Titel The Arab Spring and Climate Change – A Climate and Security Correlations Series [2] vom Februar 2013 im pdf-Format. Die Hitzewelle in Russland war danach nur ein Faktor von vielen.
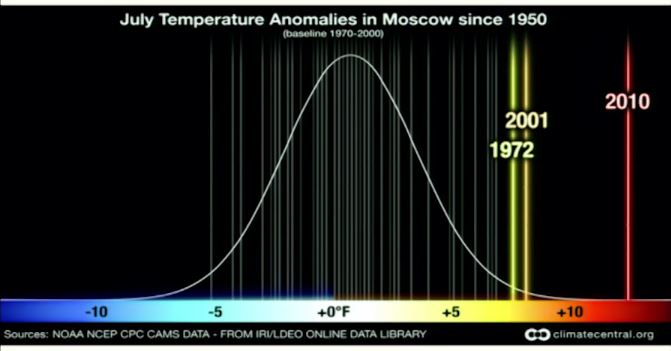
Prof. Thomas Homer-Dixon erwähnt und erläutert unter anderem das Beispiel der Hitzewelle in Moskau in seinem Vortrag der Andrews Initiative, an der Universität von Neu Braunschweig, am 19. März 2013 [3] etwa ab Position [0:22:10]. Dazu hier die grafische Darstellung der jeweils durchschnittlichen Temperaturen im Juli in Moskau. Jeder der senkrechten Balken stellt die Durchschnittstemperatur eines Jahres dar. Die Kurve zeigt die sogenannte Gaußsche Normalverteilung der Durchschnittstemperaturen und die Skala unten die Abweichung vom Mittelwert in Grad Fahrenheit. Wie man sieht, häufen sich die Werte in der Mitte. Zum Thema Normalverteilung und Standardabweichung siehe den zugehörigen Wikipediaeintrag [4].
 [5]
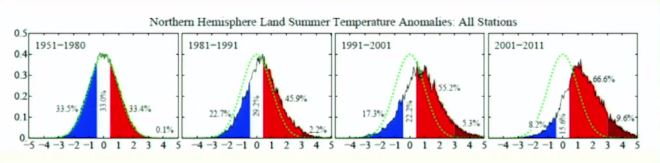
[5]Eine Erklärung für die zunächst als extrem unwahrscheinlich eingestufte Temperatur im Juli 2010 liefert die von Homer-Dixon erwähnte Arbeit von James E. Hansen [6], Makiko Sato und Reto Ruedy. Homer-Dixon hatte für seinen Vortrag eine vorläufige Version dieses Artikels benutzt, die noch den Titel “Climate Variability and Climate Change: The New Climate Dice“. Ab Position [25:37] zeigt er daraus folgende Grafik zeigt:
 [7]
[7]Hansen war bis 2013 leitender Wissenschaftler für Klimatologie bei der NASA. Der endgültige Artikel hat den Titel Perceptions of Climate Change: The New Climate Dice. Hier die Kurzversion der NASA: Science Briefs: The New Climate Dice: Public Perception of Climate Change [8] und hier ein Link auf die 13-seitige Langversion für Wissenschaftler [9]. Die Grafik zeigt die durchschnittliche Sommertemperatur über Land, im Mittel aller Messstationen, auf der nördlichen Halbkugel. Die farbigen Flächen repräsentieren die Landfläche. Die Ziffern unten, von -5 bis 5, geben die Anzahl der Standardabweichungen bezogen auf die Normalverteilung der Durchschnittstemperatur in den Jahren 1951 – 1980 wieder. Der Tabelle aus dem Wikipediaeintrag zur Normalverteilung und Standardabweichung habe ich dazu die folgenden Wahrscheinlichkeiten für entnommen:
| Anzahl Standardabweichungen in (σ)(sprich “Sigma”) | Wahrscheinlichkeit das ein Wert ausserhalb der Grenze liegt, als Bruchteil angegeben |
| 1 | 1 / 3,151 |
| 2 | 1 / 21,977 |
| 3 | 1 / 370,4 |
| 4 | 1 / 15.787 |
| 5 | 1 / 1.744.278 |
Die grün gepunktete Kurve ist die Normalverteilung der Durchschnittstemperatur in den Jahren 1951 bis 1980. Die drei rechten Grafiken geben jeweils die Verteilung der Temperaturen in den 10-Jahreszeiträumen 1981 – 1991, 1991 – 2001 und 2001 – 2011 wieder. Wie man sieht, verschiebt sich die Kurve und es werden, bezogen auf die Werte von 1951 – 1981, für einen immer größeren Teil der Landfläche “extrem unwahrscheinliche” Werte, also solche mit 3 und sogar mit mehr als 4-facher Standardabweichung erreicht. 3-fach heißt dabei nach obiger Tabelle “einmal in 370 Jahren zu erwarten” und 4-fach heißt einmal in 15.787 Jahren zu erwarten.
An Position [30:15] zeigt er eine Folie mit dem daraus resultierenden Statement von Hansen und Mitarbeitern, deren Text ich hier übersetze:
Von 1951 bis 1961 kam es im Sommer auf 0,23 Prozent der Landfläche zu Hitzeextremen mit mehr als drei Standardabweichungen (σ)(sprich “Sigma”) von der Durchschnittstemperatur. Nun betreffen solche Hitzewellen im Sommer ungefähr 10 Prozent der Landfläche. Das ist eine 30-fache Steigerung in 50 Jahren. “Wenn die Geschwindigkeit der globalen Erwärmung nicht vermindert wird, dann werden Mitte dieses Jahrhunderts 3- σ Ereignisse (sprich 3-Sigma-Ereignisse) die neue Normalität und 5- σ Ereignisse gewöhnlich sein.
Die statistische Normalverteilung, mit der solche Wahrscheinlichkeiten berechnet werden, funktioniert nämlich nur dann wie erwartet, wenn man tatsächlich zufällige Ereignisse misst. Wenn sich, wie hier beim Klima, für das Messergebnis grundlegende Werte sehr langsam und möglicherweise dazu auch noch mit wiederum von Zufällen abhängender Geschwindigkeit in eine Richtung verändern, überlagern sich diese Veränderung mit den üblichen zufälligen Schwankungen der Messergebnisse.
Die Folge ist, dass auf den ersten Blick extrem unwahrscheinliche Messwerte in Richtung der sich überlagernden langsamen Veränderung tatsächlich sehr viel wahrscheinlicher sein können, als man aus den Daten der Vergangenheit berechnet hat. Man bedenke dabei auch, dass solche plötzlich beginnenden, langsamen Veränderungen bei ihrem Beginn in der Regel zunächst unbekannt sind und daher auch nicht berücksichtigt werden können.
Solche langsamen und möglicherweise unbemerkt beginnenden Veränderungen von Teilen komplexer Systeme (siehe dazu Eigenschaften einfacher Maschinen und Komplexer Systeme [10]), die im Mittel viel kleiner als die zufällige Schwankung der Messwerte ist, können jedenfalls dazu führen, dass vermeintlich sehr unwahrscheinliche Ereignisse in Wirklichkeit längst sehr wahrscheinlich sind.
Eine weiteres, allgemein oft nicht bedachtes Problem, auf das Prof. Thomas Homer-Dixon in seinem oben erwähnten Vortrag kurz eingeht, dass die wichtigen Getreidesorten beim Überschreiten bestimmter Temperaturgrenzen in bestimmten Wachstumsphasen schlagartig drastisch an Ertragskraft verlieren. Während man bisher im allgemeinen gedacht habe, dass der Klimawandel durch Temperatursteigerung und zunehmenden CO2-Gehalt der Luft die Ernten steigern könnte, ist eher damit zu rechnen, dass es zu plötzlichen Einbrüchen der Ernten komme.
Solche Phänomene sind als Kippunkt, Umschlagpunkt oder Tipping Point [11]bekannt. Ein System kann bis zum Erreichen eines Kippunktes scheinbar bestens funktionierten und dann plötzlich vollständig versagen oder vollständig anders reagieren. Auch dieses Phänomen kann dafür sorgen, dass ein scheinbar extrem unwahrscheinliches Ereignis tatsächlich extrem wahrscheinlich bis sicher eintreten wird.
Man stelle sich vor, dass man eine wichtige Messgrösse seit langem beobachtet, dann auf Grund der Messungen Voraussagen über zu erwartende zukünftige Messwerte macht, während man nichts davon ahnt (oder wissen will), dass man sich einem Kippunkt nähert. Selbst unmittelbar vor dem Erreichen des Kippunktes wird ein hinreichend ignoranter “Experte” mit Blick auf die bisherigen Messungen mit gutem Gewissen behaupten, dass die in der Realität dann schon kurz noch dem Überschreiten des Kippunktes gemessenen Werte extrem unwahrscheinlich oder sogar völlig ausgeschlossen sind.
Gute Beispiele für diese Phänomen sind alle Tiere, die in freiwillig in eine Falle laufen sowie alle Tiere, die auf der Jagd vom Ansitz aus erlegt werden. Damit ein Jäger ein Reh vom Hochsitz aus erlegen kann, ist es zwingend notwendig, dass das Reh die Situation für ausreichend sicher hält, obwohl sie das nicht mehr ist.
In der Praxis kann das Ignorieren solcher eigentlich trivialen Einsichten durchaus zum Untergang ganzer Völker und Zivilisationen führen, weil kostbare Zeit und Ressourcen verschwendet wurden, als noch Zeit und Möglichkeiten für wirksame Gegenmaßnahmen vorhanden waren.
Kelberg, den 12. Mai 2017
Christoph Becker
